Basic syntax and variables
Types of parallel problems
The basic concept of parallel computing is simple to understand: we divide our job into tasks that can be executed at the same time, so that we finish the job in a fraction of the time that it would have taken if the tasks are executed one by one.
Task is a unit of computation that can run in parallel with other tasks. In this course, we’ll be using a more general term “task” that – depending on the context – could mean either a Unix process (MPI task or rank) or a Unix thread. Consequently, parallel execution in Chapel could mean either multiprocessing and multithreading, or both (hybrid parallelism). In Chapel in many cases this distinction is hidden from the programmer.
Implementing parallel computations is not always easy. How easy it is to parallelize a code really depends on the underlying problem you are trying to solve. This can result in:
- a fine-grained, or tightly coupled parallel code that needs a lot of communication / synchronization between tasks, or
- a coarse-grained code that requires little communication between tasks.
In this sense grain size refers to the amount of independent computing in between communication events. An extreme case of a coarse-grained problem would be an embarrassing parallel problem where all tasks can be executed completely independent from each other (no communications required).
In the non-GPU part of this course we’ll be solving two numerical problems:
- Julia set is an embarrassingly parallel problem (no communication between tasks), and
- heat diffusion is a tightly coupled problem that requires communication between tasks at each step of the iteration.
We’ll start with a serial of the Julia set and will use it to learn the basics of Chapel.
Case study 1: computing the Julia set
This project is a mathematical problem to compute a Julia set, defined as a set of points on the complex plane that remain bound under infinite recursive transformation \(f(z)\). We will use the traditional form \(f(z)=z^2+c\), where \(c\) is a complex constant. Here is our algorithm:
- pick a point \(z_0\in\mathbb{C}\)
- compute iterations \(z_{i+1}=z_i^2+c\) until \(|z_i|>4\) (arbitrary fixed radius; here \(c\) is a complex constant)
- store the iteration number \(\xi(z_0)\) at which \(z_i\) reaches the circle \(|z|=4\)
- limit max iterations at 255
4.1 if \(\xi(z_0)=255\), then \(z_0\) is a stable point
4.2 the quicker a point diverges, the lower its \(\xi(z_0)\) is - plot \(\xi(z_0)\) for all \(z_0\) in a rectangular region \(-1<=\mathfrak{Re}(z_0)<=1\), \(-1<=\mathfrak{Im}(z_0)<=1\)
We should get something conceptually similar to this figure (here \(c = 0.355 + 0.355i\); we’ll get drastically different fractals for different values of \(c\)):
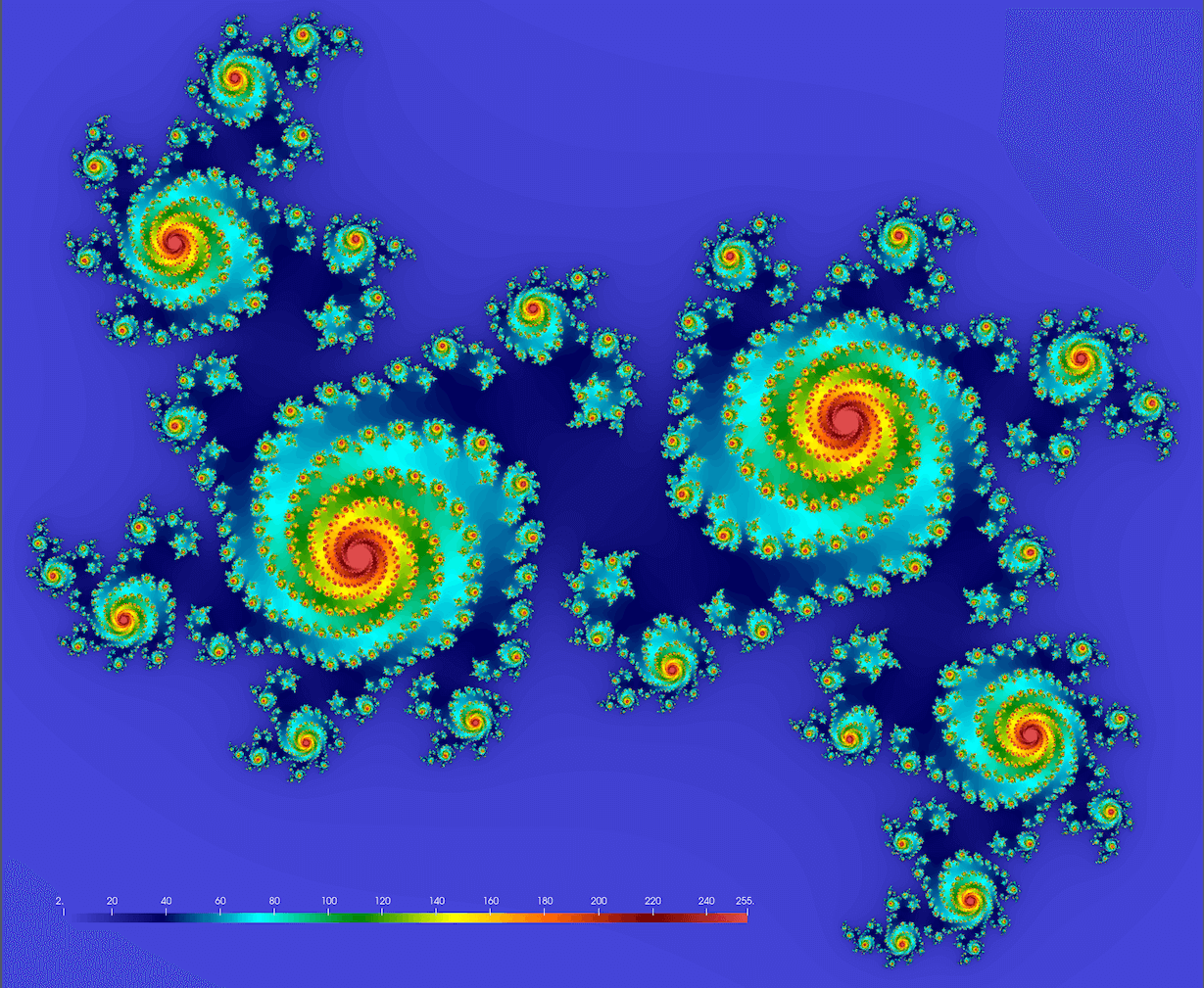
You might want to try these values too:
\(c = 1.2e^{1.1πi}\) \(~\Rightarrow~\) original textbook example
\(c = -0.4-0.59i\) and 1.5X zoom-out \(~\Rightarrow~\) denser spirals
\(c = 1.34-0.45i\) and 1.8X zoom-out \(~\Rightarrow~\) beans
\(c = 0.34-0.05i\) and 1.2X zoom-out \(~\Rightarrow~\) connected spiral boots
Variables
Chapel is a statically typed language, i.e. the type of every variable must be known at compile time.
Variables in Chapel are declared with the var or const keywords. When a variable declared as const is initialized, its value cannot be modified anymore during the execution of the program.
To declare a variable, we must either (1) specify its type or (2) initialize it in place with some value from which the compiler will infer its type. The common variable types in Chapel are:
- integer
int– defaults toint(64), or you can explicitly specifyint(32), - floating point number
real– defaults toreal(64), or you can explicitly specifyreal(32), - boolean
bool, - string
string
If a variable is declared without a type, Chapel will infer it from the given initial value, for example (let’s store this in juliaSetSerial.chpl):
const n = 2_000; // vertical and horizontal size of our imageAll these constant variables will be created as integers, and no other values can be assigned to these variables during the execution of the program.
On the other hand, if a variable is declared without an initial value, Chapel will initialize it with a default value depending on the declared type:
var y: real; // vertical coordinate in our plot; real(64) variable set to 0.0
var point: complex; // current point in our image; complex(64) variable set to 0.0+0.0*1iOf course, we can use both, the initial value and the type, when declaring a varible as follows:
const c: complex = 0.355 + 0.355i; // Julia set constantThe following two notations are different, but produce the same result in the end:
var a: real = 10; // we specify both the type and the value
var a = 10: real; // we specify only the value (integer 10 converted to real)Let’s print our configuration after we set all parameters:
writeln('Computing ', n, 'x', n, ' Julia set ...');Alternatively, you can use formatted output:
writef("Computing %ix%i Julia set\n", n, n);For other format specifiers, check the table at https://chapel-lang.org/docs/modules/standard/IO/FormattedIO.html
Printing variable’s type
To check a variable’s type, use .type query:
var x = 1e8:int;
type t = x.type;
writeln(t:string);or in a single line:
writeln((1e8:int).type:string);
writeln((0.355 + 0.355i).type: string);